Michael的笔记本

全文检索

所以在了解Lucene之前要费一番工夫了解一下全文检索。

那么什么叫做全文检索呢？这要从我们生活中的数据说起。

我们生活中的数据总体分为两种：结构化数据和 非结构化数据 。

• 结构化数据： 指具有固定格式或有限长度的数据，如数据库，元数据等。
• 非结构化数据： 指不定长或无固定格式的数据，如邮件，word文档等。

当然有的地方还会提到第三种，半结构化数据，如XML，HTML等，当根据需要可按结构化数据来处理，也可抽取出纯文本按非结构化数据来处理。

非结构化数据又一种叫法叫全文数据。

按照数据的分类，搜索也分为两种：

• 对结构化数据的搜索 ：如对数据库的搜索，用SQL语句。再如对元数据的搜索，如利用windows搜索对文件名，类型，修改时间进行搜索等。
• 对非结构化数据的搜索 ：如利用windows的搜索也可以搜索文件内容，Linux下的grep命令，再如用Google和百度可以搜索大量内容数据。

对非结构化数据也即对全文数据的搜索主要有两种方法：

• 顺序扫描法(Serial Scanning)： 所谓顺序扫描，比如要找内容包含某一个字符串的文件，就是一个文档一个文档的看，对于每一个文档，从头看到尾，如果此文档包含此字符串，则此文档为我们要找的文件，接着看下一个文件，直到扫描完所有的文件。
• 全文检索(Full-text Search)： 将非结构化数据中的一部分信息提取出来，重新组织，使其变得有一定结构，然后对此有一定结构的数据进行搜索，从而达到搜索相对较快的目的，这部分从非结构化数据中提取出的然后重新组织的信息，我们称之 索引 。

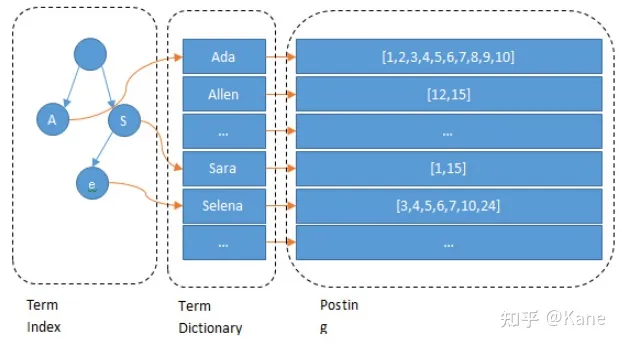
左边保存的是一系列字符串，称为 词典 。

每个字符串都指向包含此字符串的文档(Document)链表，此文档链表称为 倒排表 (Posting List)。

这部分对有基础的应该很快熟悉，所以不过多介绍

来看看Lucene是怎样存储索引文件格式

Lucene的文件扩展名摘要

首先，要像了解lucene是怎样存储的，可以看看存储文件：

Lucene的索引结构中，即保存了正向信息，也保存了反向信息。

所谓正向信息：

• 按层次保存了从索引，一直到词的包含关系：索引(Index) –> 段(segment) –> 文档(Document) –> 域(Field) –> 词(Term)（这些概念稍后会介绍）
• 也即此索引包含了哪些段，每个段包含了那些文档，每个文档包含了那些域，每个域包含了那些词。
• 既然是层次结构，则每个层次都保存了本层次的信息以及下一层次的元信息，也即属性信息。
• 如上图，包含正向信息的文件有：
  • segments_N保存了此索引包含多少个段，每个段包含多少篇文档。
  • .fnm保存了此段包含了多少个域，每个域的名称及索引方式。
  • .fdx，.fdt保存了此段包含的所有文档，每篇文档包含了多少域，每个域保存了那些信息。
  • .tvx，.tvd，.tvf保存了此段包含多少文档，每篇文档包含了多少域，每个域包含了多少词，每个词的字符串，位置等信息。

所谓反向信息：

• 保存了词典到倒排表的映射：词(Term) –> 文档(Document)
• 如上图，包含反向信息的文件有：
  • .tis，.tii保存了词典(Term Dictionary)，也即此段包含的所有的词按字典顺序的排序。
  • .frq保存了倒排表，也即包含每个词的文档ID列表。
  • .prx保存了倒排表中每个词在包含此词的文档中的位置。

索引文件结构

• 索引（index）
  • Lucene的索引由许多个文件组成，这些文件放在同一个目录下
• 段（segment）
  • 一个Lucene的索引由多个段组成，段与段之间是独立的。添加新的文档时可以生成新的段，达到阈值（段的个数，段中包含的文件数等）时，不同的段可以合并。
  • 在文件夹下，具有相同前缀的文件属于同一个段
  • segments.gen 和 segments_N（N表示一个具体数字，eg：segments_5）是段的元数据文件，他们保存了段的属性信息。
• 文档（document）
  • 文档时建索引的基本单位，一个段中可以包含多篇文档
  • 新添加的文档时单独保存在一个新生成的段中，随着段的合并，不同的文档会合并到至相同的段中。
• 域（Field）
  • 一个文档有可由多个域（Field）组成，比如一篇新闻，有 标题，作者，正文等多个属性，这些属性可以看作是文档的域。
  • 不同的域可以指定不同的索引方式，比如指定不同的分词方式，是否构建索引，是否存储等
• 词（Term）
  • 词 是索引的最小单位，是经过词法分词和语言处理后的字符串

索引存储规则

了解完文件结构，再来了解一下 存储规则 ：

Lucene为了使的信息的存储占用的 空间更小 ，访问 速度更快 ，采取了一些特殊的技巧

1，引入Term Index 层

为了能快速找到某个term，将所有的term排个序， 二分法查找term ，logN的查找效率，就像通过字典查找一样，这就是 Term Dictionary（ 这是第一步的加速）。现在再看起来，似乎和传统数据库通过B-Tree的方式类似啊，为什么说比B-Tree的查询快呢？

B-Tree通过减少磁盘寻道次数来提高查询性能，Lucene也是采用同样的思路，直接通过内存查找term，不读磁盘，但是如果term太多，term dictionary也会很大，放内存不现实，于是有了 Term Index（ 这是第二步的加速），就像字典里的索引页一样，A开头的有哪些term，分别在哪页，可以理解term index是一颗树。

这棵树不会包含所有的term，它包含的是term的一些 前缀 。通过term index可以快速地定位到term dictionary的某个offset，然后从这个位置再往后顺序查找。如下图：

实际上存储：

比如要存储如下词:

term
termagancy
termagant
terminal

如果按照正常方式来存储，需要的空间如下：

[VInt = 4] [t][e][r][m]
[VInt = 10][t][e][r][m][a][g][a][n][c][y]
[VInt = 9][t][e][r][m][a][g][a][n][t]
[VInt = 8][t][e][r][m][i][n][a][l]

共需要35个Byte.

如果应用前缀后缀规则，需要的空间如下：

[VInt = 4] [t][e][r][m]
[VInt = 4 (offset)][VInt = 6][a][g][a][n][c][y]
[VInt = 8 (offset)][VInt = 1][t]
[VInt = 4(offset)][VInt = 4][i][n][a][l]

共需要22个Byte。

大大缩小了存储空间，尤其是在按字典顺序排序的情况下，前缀的重合率大大提高。

2， posting list的压缩

对posting list有压缩，有俩种压缩方式：

• 增量编码压缩（Frame Of Reference ） ，将大数变小数，按字节存储

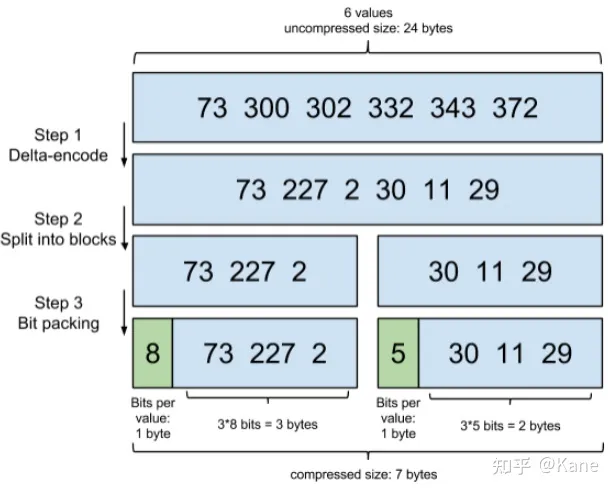
原理就是通过增量，将原来的大数变成小数仅存储增量值，再精打细算按bit排好队，最后通过字节存储，而不是大大咧咧的尽管是2也是用int(4个字节)来存储

比如要存储如下整数：

16386
16387
16388
16389

如果按照正常方式来存储，需要的空间如下：

[(1) 000, 0010][(1) 000, 0000][(0) 000, 0001]
[(1) 000, 0011][(1) 000, 0000][(0) 000, 0001]
[(1) 000, 0100][(1) 000, 0000][(0) 000, 0001]
[(1) 000, 0101][(1) 000, 0000][(0) 000, 0001]

供需12个Byte。

如果应用差值规则来存储，需要的空间如下：

[(1) 000, 0010][(1) 000, 0000][(0) 000, 0001]
[(0) 000, 0001]
[(0) 000, 0001]
[(0) 000, 0001]

共需6个Byte。

大大缩小了存储空间，而且无论是文档ID，还是词在文档中的位置，都是按从小到大的顺序，逐渐增大的。

• Roaring bitmaps

说到Roaring bitmaps，就必须先从bitmap说起。Bitmap是一种数据结构，假设有某个posting list：

[1,3,4,7,10]

对应的bitmap就是：

[1,0,1,1,0,0,1,0,0,1]

非常直观，用0/1表示某个值是否存在，比如10这个值就对应第10位，对应的bit值是1，这样用一个字节就可以代表8个文档id，旧版本(5.0之前)的Lucene就是用这样的方式来压缩的，但这样的压缩方式仍然不够高效，如果有1亿个文档，那么需要12.5MB的存储空间，这仅仅是对应一个索引字段(我们往往会有很多个索引字段)。于是有人想出了Roaring bitmaps这样更高效的数据结构。

Bitmap的缺点是存储空间随着文档个数线性增长，Roaring bitmaps需要打破这个魔咒就一定要用到某些指数特性：

将posting list按照65535为界限分块，比如第一块所包含的文档id范围在0~65535之间，第二块的id范围是65536~131071，以此类推。再用 <商，余数> 的组合表示每一组id，这样每组里的id范围都在0~65535内了，剩下的就好办了，既然每组id不会变得无限大，那么我们就可以通过最有效的方式对这里的id存储。

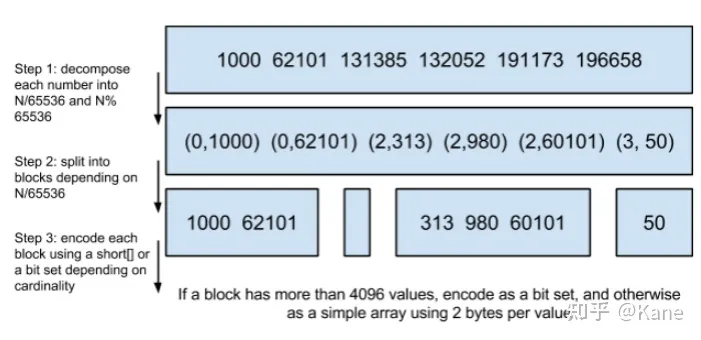
细心的小明这时候又举手了:"为什么是以65535为界限?"

程序员的世界里除了1024外，65535也是一个经典值，因为它= 2^16-1 ，正好是用2个字节能表示的最大数，一个short的存储单位，注意到上图里的最后一行“If a block has more than 4096 values, encode as a bit set, and otherwise as a simple array using 2 bytes per value”，如果是大块，用节省点用bitset存，小块就豪爽点，2个字节我也不计较了，用一个short[]存着方便。

那为什么用4096来区分大块还是小块呢？

个人理解：都说程序员的世界是二进制的，4096*2bytes ＝ 8192bytes < 1KB, 磁盘一次寻道可以顺序把一个小块的内容都读出来，再大一位就超过1KB了，需要两次读。

3，term index的压缩

Lucene使用FST算法以字节的方式来存储所有的Term，重复利用Term Index的前缀和后缀，使Term Index小到可以放进内存，减少存储空间，不过相对的也会占用更多的cpu资源。FST在Lucene4.0以后的版本中用于快速定位所查单词在字典中的位置。
Finite StateTransducers，简称 FST，通常中文译作 有穷状态转换器 ，在语音识别和自然语言搜索、处理等方向被广泛应用。
FST的功能类似于字典，可以表示成FST<Key, Value>的形式。其最大的特点是，可以用O(length(key))的复杂度来找到key对应的value，也就是说查找复杂度仅取决于所查找的key长度。
假设我们现在要将以下term index映射到term dictionary的block序号：

cat—— > 5
deep —— > 10
do —— > 15
dog —— > 2
dogs —— > 8

最简单的做法就是定义个Map<string, integer="">，大家找到自己的位置对应入座就好了，但从内存占用少的角度想想，有没有更优的办法呢？答案就是FST。
对于经典FST算法来说，要求Key必须按字典序从小到大加入到FST中。上面的例子中key已经排好序了。
按照以下步骤建立FST：

 1.建一个空节点，表示FST的入口，所有的Key都从这个入口开始。
 2.如果还有未处理的Key，则枚举Key的每一个label。处理流程如下：
  2.1如果当前节点存在含此label的边，则
      2.1.1如果Value包含该边的out值，则
              Value = Value – out
      2.1.2否则
                   令temp=out–Value；
                   out =Value，并使下一个节点的所有边out都加上temp。
                   如果下一节点是Final节点 则FinalOut += temp
      2.1.3进入下一个节点
  2.2否则： 新建一个节点另其out = Value， Value = 0。
 

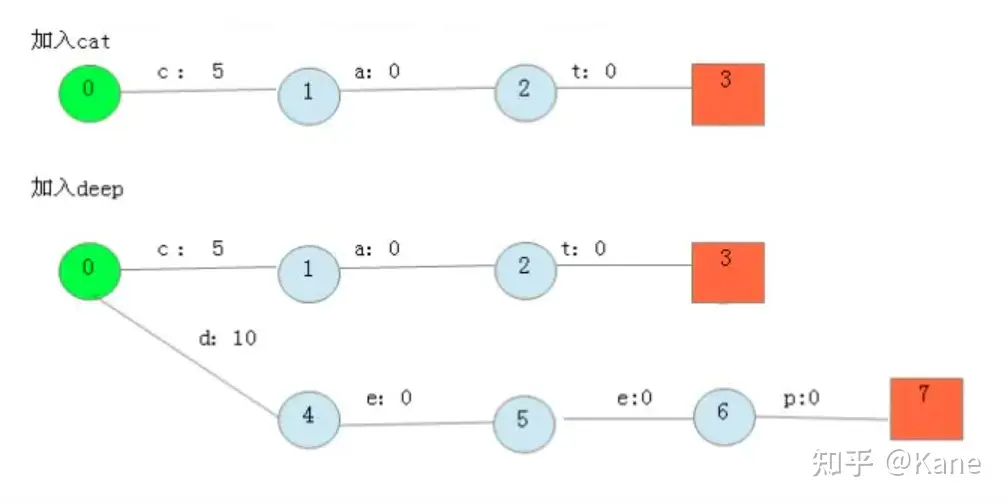
最后加入dogs，得到最后的结果：

从上图可以看出，每条边有两条属性，一个表示label（key的元素），另一个表示Value(out)。注意Value不一定是数字，还可一是另一个字符串，但要求Value必须满足叠加性，如这里的正整数2 + 8 = 10。字符串的叠加行为： aa + b = aab。
建完这个图之后，我们就可以很容易的查找出任意一个key的Value了。例如：查找dog，我们查找的路径为：0 → 4 → 8 → 9。 其权值和为： 2 + 0 + 0 + 0 = 2。其中最后一个零表示 node[9].finalOut = 0。所以“dog”的Value为2。

4，跳跃表规则(Skip list)

为了提高查找的性能，Lucene在很多地方采取的跳跃表的数据结构。

跳跃表(Skip List)是如图的一种数据结构，有以下几个基本特征：

• 元素是按顺序排列的，在Lucene中，或是按字典顺序排列，或是按从小到大顺序排列。
• 跳跃是有间隔的(Interval)，也即每次跳跃的元素数，间隔是事先配置好的，如图跳跃表的间隔为3。
• 跳跃表是由层次的(level)，每一层的每隔指定间隔的元素构成上一层，如图跳跃表共有2层。

需要注意一点的是，在很多数据结构或算法书中都会有跳跃表的描述，原理都是大致相同的，但是定义稍有差别：

• 对间隔(Interval)的定义 ： 如图中，有的认为间隔为2，即两个上层元素之间的元素数，不包括两个上层元素；有的认为是3，即两个上层元素之间的差，包括后面上层元素，不包括前面的上层元素；有的认为是4，即除两个上层元素之间的元素外，既包括前面，也包括后面的上层元素。Lucene是采取的第二种定义。
• 对层次(Level)的定义 ：如图中，有的认为应该包括原链表层，并从1开始计数，则总层次为3，为1，2，3层；有的认为应该包括原链表层，并从0计数，为0，1，2层；有的认为不应该包括原链表层，且从1开始计数，则为1，2层；有的认为不应该包括链表层，且从0开始计数，则为0，1层。Lucene采取的是最后一种定义。

跳跃表比顺序查找，大大提高了查找速度，如查找元素72，原来要访问2，3，7，12，23，37，39，44，50，72总共10个元素，应用跳跃表后，只要首先访问第1层的50，发现72大于50，而第1层无下一个节点，然后访问第2层的94，发现94大于72，然后访问原链表的72，找到元素，共需要访问3个元素即可。

原文链接https://zhuanlan.zhihu.com/p/443722667